Hi, my name is Mike and I'm a recovering physicist. Or I was until I found this video.
OK, this one isn't going to be to everyone's taste, but I assure you it's fun. How do you control a ball inside a wheel when you only have control over the rotation of the wheel?
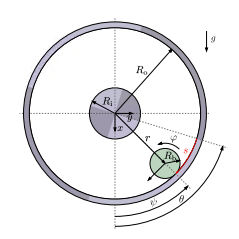

Control theory is fascinating and it is all based on mechanics, linear systems, and well you get the idea. If you know some physics, aren't too afraid of math and know how to program then it could be your new hobby. Certainly building the hoop and ball system isn't beyond the capabilities of anyone happy to use a Raspberry Pi to control a motor. The designers, Martin Gurtner and Jiří Zemánek of the Czech Technical University in Prague, have provided all the details of how to build it on Github, complete with the software:
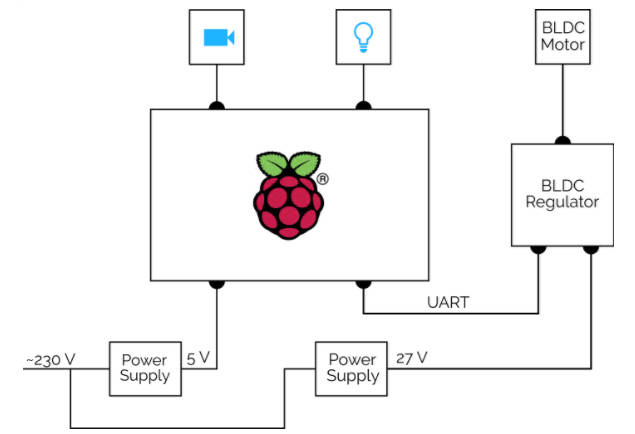
In this case the reason for the fun, I mean serious research, is partly to enter the IEEE CSS Video Clip Contest and partly to demonstrate the advanced technique of numerical optimal control. The video is interesting because it explains how things work and it isn't afraid to show when things go wrong.
Take a look the first trick which is to get the ball to make a complete loop, and there is a slow motion demo towards the end where you get to see what is happening in much more detail:
If you want to know more there is a paper that explains it in great detail and outlines an even more impressive trick - getting the ball to land on the inner wheel and balancing it on the inner wheel. Now that deserves a video.
The conclusion of the paper is interesting and suggests some further work:
"We showed that the well-known ball and hoop system can be used not only to demonstrate some aspects of linear control theory but also to demonstrate strengths of numerical optimal control. We extended the ball and hoop system by another hoop and described this extended system by a hybrid model. We presented two tasks for the extended system that are ideal for a demonstration of trajectory generation and stabilization and solve them. As the model of the extended system is simple, one can also use it for a demonstration of control techniques that are based on Sum-Of-Squares programming. For instance, our proposed solution of the presented tasks can be extended by LQR trees to work also for varying initial conditions. Furthermore, the inner hoop can be replaced by something else. For example, one can replace it by a beam and modify the Task 2 to “get the ball on a beam and stabilize it there”. Or, the inner hoop can be replaced by a figure-eight shaped rails and the “butterfly” task can be solved on the system"

More Information
GitHub: https://github.com/aa4cc/flying-ball-...
Paper: http://arxiv.org/abs/1706.07333
